Pomiary drgań: podstawy analizy
Pozyskiwanie danych wibracyjnych jest tylko częścią wyzwania pomiaru drgań; druga część to analiza uzyskanych danych. Ważne jest zrozumienie rodzajów przebiegów czasowych związanych z analizą drgań, ważnych różnic między nimi i kiedy właściwe jest użycie każdego typu narzędzia do analizy drgań. Oto krótki przegląd niektórych podstaw.
Analiza drgań w domenie czasu
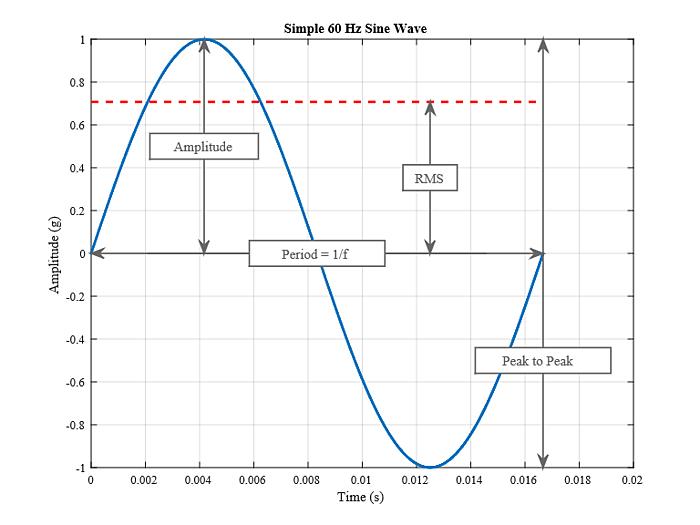
Analiza drgań rozpoczyna się od zmieniającego się w czasie sygnału rzeczywistego z przetwornika lub czujnika. Interpretacja danych dotyczących drgań w dziedzinie czasu (amplituda wykreślona w funkcji czasu) jest ograniczona do kilku parametrów w określaniu poziomu drgań: amplitudy, wartości szczytowej i wartości skutecznej, które są identyfikowane w przebiegu sinusoidalnym.
Wartość szczytowa lub amplituda jest istotna dla zdarzeń impulsowych, ale nie uwzględnia czasu trwania, a tym samym energii w zdarzeniu.
To samo odnosi się do wartości szczytowej z dodatkową korzyścią polegającą na zapewnieniu maksymalnego wychylenia przebiegu. Jest to przydatne podczas przeglądania informacji o przemieszczeniu, w szczególności luzów.
Wartość RMS jest na ogół najbardziej użyteczna, ponieważ jest bezpośrednio związana z poziomem energii drgań, a tym samym z destrukcyjną wielkością wibracji.
Wibracja jest ruchem oscylacyjnym, więc większość analiz drgań ma na celu określenie szybkości tej oscylacji lub częstotliwości. Liczba wystąpień pełnego cyklu ruchu w okresie jednej sekundy jest częstotliwością drgań i jest mierzona w Hz. W przypadku prostych fal sinusoidalnych częstotliwość drgań można określić na podstawie obserwacji przebiegu w dziedzinie czasu; jednak, gdy dodawane są różne składowe częstotliwości i szumy, analiza widma jest niezbędna do uzyskania wyraźniejszego obrazu częstotliwości drgań.
Analiza drgań w domenie częstotliwości
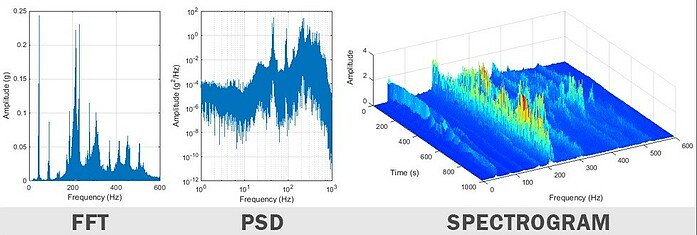
Szybka transformata Fouriera (FFT)
Szybka transformata Fouriera (FFT) jest wydajnym algorytmem używanym do obliczania dyskretnej transformaty Fouriera (DFT). Ta transformata Fouriera wyprowadza amplitudę drgań jako funkcję częstotliwości, dzięki czemu analizator może wskazać, przyczyny drgań. Rozdzielczość częstotliwości w FFT jest wprost proporcjonalna do długości sygnału i częstotliwości próbkowania. Aby poprawić rozdzielczość, czas nagrania musi zostać wydłużony, ale należy uważać na zmieniające się środowisko wibracji.
Spektrogram
Spektrogram pobiera szereg widm FFT, aby zilustrować, jak zmienia się widmo (domena częstotliwości) w czasie. Jeśli analiza drgań jest przeprowadzana w zmieniającym się środowisku, spektrogram będzie potężnym narzędziem do zilustrowania, jak dokładnie zmienia się to widmo drgań.
Gęstość widmowa mocy
Gęstość widmowa mocy (PSD) przyjmuje amplitudę FFT, mnoży ją przez złożoną koniugację i normalizuje ją do szerokości przedziału częstotliwości. Pozwala to na dokładne porównanie sygnałów drgań losowych, które mają różne długości sygnału. Z tego powodu PSD jest zwykle używana do opisywania środowiska drgań losowych, takich jak określone w wojskowych i komercyjnych standardach testowych.